Effektiver Druck
Effektiver Druck und spezifische Mahlkraft
Die Druckverteilung im Spalt ist zweidimensional und der Zerkleinerungseffekt deshalb in verschiedenen Walzenebenen unterschiedlich, s. Abb. 57. Es erscheint sinnvoll, den effektiven Druck peff, wie er im vorangegangenen Kapitel Axiale Druckverteilung eingeführt wurde, als ein Maß für die Beanspruchungsintensität zu betrachten und ihn mit der bereits in zwei früheren Arbeiten wurde diese Verknüpfung mit dem Ziel untersucht, den maximalen Druck pm abzuschätzen [21],[22],[2]. Über die axiale Druckverteilung lagen damals keine quantitativen Erkenntnisse vor, deswegen wurde diese nicht berücksichtigt und nachstehende vereinfachte Ableitung entwickelt:
dF = (D L / 2) p(a) cosa da

Unter der Voraussetzung, dass der Kompressionswinkel a0 und der Rückdehnwinkel g klein bleiben, kann der cosa gleich eins gesetzt werden. Die Druckverteilung wird durch das Produkt aus Maximaldruck pm und einer Winkelfunktion f(a) dargestellt.
dF = (D L / 2) pm f(a) da
Das Ergebnis der Integration lässt sich wie folgt schreiben:
Fsp = pm a0 cF
Der Wert von cF ergibt sich aus der Integration des Druckdiagramms und entspricht dem weiter unten in Gleichung 21 enthaltenen I(k). Das in [21],[22] angegebene Resultat folgt aus den drei Voraussetzungen: (1.) Approximation der Druckverteilung durch eine Potenzfunktion mit Maximum bei a = 0, (2.) Variation des Exponenten zwischen drei und fünf, (3.) Vernachlässigung der Rückdehnung. Der Wert von cF liegt zwischen 0,19 und 0,23. Für eine erste Abschätzung von pm wird cF = 0,2 vorgeschlagen. In [2] wird die in Kapitel Druckverteilung im Walzenspalt zitierte Kompressionsfunktion
q = 1 – exp [ -(p/pc)n]
eingeführt und eine Rückdehnung zwischen 0 und 5 % berücksichtigt. Die Ergebnisse sind in der Form von Diagrammen angegeben, aus denen bei einer Rückdehnung von 5 % cF-Werte zwischen 0,22 und 0,31 resultieren.
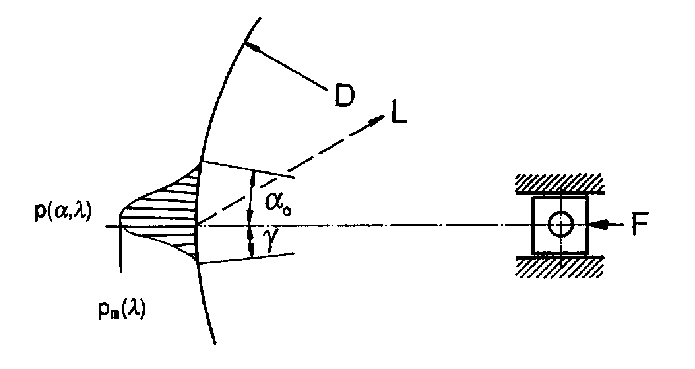
Ausgehend von der zweidimensionalen Druckverteilung p(a,l) stellt sich die Ableitung folgendermaßen dar, s. Abbildung unten:
d2F = (D L / 2) p(a,l) cosa da dl (16)
Auch hier wird der Kosinus gleich eins gesetzt. Die spezifische Mahlkraft ergibt sich dann nach zweifacher Integration zu:
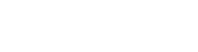 (17)
(17)
Skizze zur Verknüpfung des effektiven Druckes mit der spezifischen Mahlkraft
Zur Berechnung des Integrals müssen p(a,l) sowie die Winkel a0 und g bekannt sein. Hierbei ergibt sich die Schwierigkeit, dass a0 und g prinzipiell sowohl von l als auch von der spezifischen Mahlkraft abhängen können. Die Untersuchungen haben jedoch nur sehr schwache Abhängigkeiten gezeigt, so soll für die weitere Ableitung deren Unabhängigkeit von l, und Fsp angenommen werden. Aus den Untersuchungen geht weiter hervor - und dies wird später nachgewiesen -, dass die Druckverteilung in erster Annäherung als ein Produkt zweier einparametriger Funktionen dargestellt werden kann; aus dem Doppelintegral entsteht dann ein Produkt von zwei Einfachintegralen.
p(a,l) = pm(l) f(a) (18)
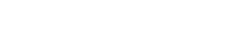 (19)
(19)
Das erste Integral ist die Bestimmungsgleichung für den effektiven Druck peff:
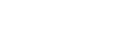 (20)
(20)
Die axiale Druckvertellung wird sicherlich von den Verhältnissen Walzenlänge zu Walzendurchmesser und Walzendurchmesser zu Partikelgröße sowie von der geometrischen Situation am Walzenrand beeinflusst; der effektive Druck hängt deshalb prinzipiell von diesen Größen ab:
peff = peff (L/D, D/x, Rand)
Diese Einflüsse sind noch unbekannt und erfordern systematische Untersuchungen.
Es wird die normierte Winkelkoordinate q = a/a0 eingeführt und das Verhältnis (g/a0) mit k bezeichnet, woraus folgt:
![]() (21)
(21)
Damit liegt eine Bestimmungsgleichung für den Integralausdruck l(k) vor.
I(k) = Fsp / peff a0 (22)
Der lntegralausdruck l(k), der die Proportionalität zwischen Effektivdruck und spezifischer Mahlkraft darstellt, kann also aus den Messgrößen peff, Fsp, und a0 berechnet werden, s. Tabelle Effektiver Druck und Integralwert. Mit Ausnahme des ersten Wertes liegt l(k) zwischen 0,26 und 0,30, ist somit nahezu konstant und liegt gut im Bereich der Modellrechnung von [2]. Als eine mögliche Erklärung für den größten Wert von 0,4 für die spezifische Mahlkraft von 1,5 N/mm2 können die größeren Schwankungen und die kleinere Anzahl der Druckmessungen angeführt werden. Gutbett-Walzenmühlen arbeiten i.a. mit einer spezifischen Mahlkraft zwischen 2,5 und 6,0 N/mm2. Für diesen Bereich ergibt sich für die untersuchten Quarz- und Kalksteinfraktionen ein von Material und Mahlkraft unabhängiger Wert.
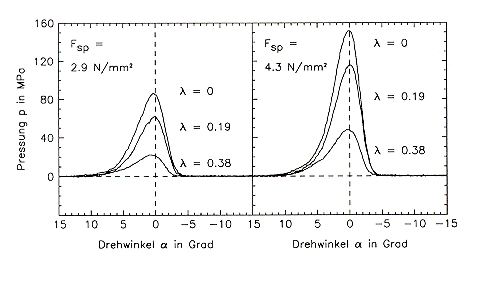
Um nachzuweisen, daß die Aufspaltung der Druckvertellung p(a,l) entsprechend Gleichung 18 zulässig ist, werden die in der obigen Abbildung dargestellten peripheren Druckverteilungen der Versuche mit der Kalksteinfraktion 1,2/1,8 mm herangezogen. Von den sechs gemessenen Druckvertellungen
p(a, li ,Fsp, j) mit l1 = 0 / l2 = 0,19 / l3 = 0,38 sowie
Fsp, 1 = 2,9 N/mm2 und Fsp, 2 = 4,3 N/mm2
werden zunächst die jeweiligen integralen Mittelwerte p(li ,Fsp, j) bestimmt.
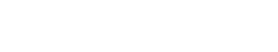
Mit diesen berechnet man das Mittel ![]() :
:
![]()
und die Normierungsfaktoren ti,j:
![]()
Die daraus folgenden normierten Druckvertellungen
pN(a, li ,Fsp, j) = p(a, li ,Fsp, j) / ti,j
sind in der nachstehenden Abbildung aufgetragen. Es zeigen sich zwar tendenzielle Abweichungen derart, dass die Druckverteilung bei l = 0,38 etwas oberhalb jener bei l = 0,19 und l = 0 verläuft und die Druckverteilungen bei der größten Mahlkraft etwas unterhalb jener der mittleren liegt. Aus den bereits im vorangegangenen Kapitel besprochenen statistischen Schwankungen ergeben sich jedoch für eine lrrtumswahrscheinlichkeit von 5 % überschneidende Vertrauensbereiche, s. zweite nachstehende Abbildung. Die eingangs geforderte Voraussetzung p(a,l) = pm(l) f(a) kann deshalb als erfüllt angesehen werden.
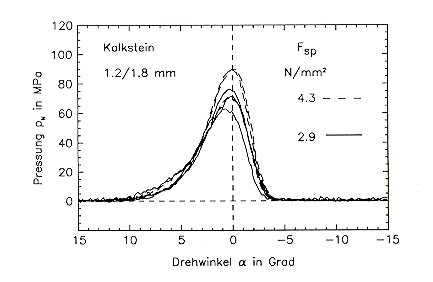
Normierte Druckdiagramme für zwei spezifische Mahlkräfte in jeweils drei verschiedenen Walzenebenen, Kalkstein 1,2/1,8 mm und u = 0,3 m/s
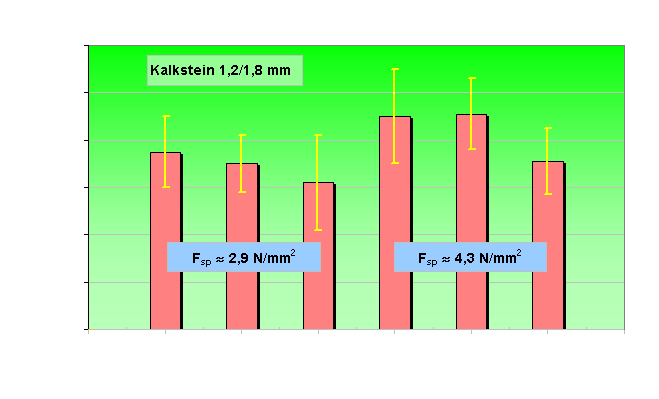
95 %-Vertrauensbereiche der normierten Druckdiagramme aus der vorherigen Abbildung